Elipse

La elipse es el lugar geométrico de los puntos del plano cuya suma de las distancias a los dos focos (puntos interiores fijos F₁ y F₂) es constante. Es decir, para todo punto a de la elipse, la suma de las distancias d₁ y d₂ es constante.

También podemos definir la elipse como una cónica, consecuencia de la intersección de un cono con un plano oblicuo que no corta la base.

Elementos de una elipse

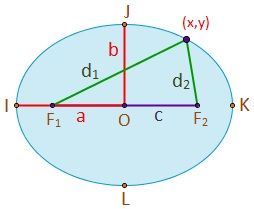
Los elementos más importante de la elipse son:

• Focos: son los puntos fijos F₁ y F₂ que generan la elipse. La suma de las dos distancias de cualquier punto de la elipse a los dos focos (d₁ y d₂) es constante.
• Distancia focal (2c): distancia entre los dos focos. F₁F₂=2c. c es la semidistancia focal.
• Centro: es el punto medio de los dos focos (O).
• Semieje mayor: longitud del segmento OI o OK (a). La longitud es mayor (o igual en el caso de la circunferencia) a la del semieje menor. La suma de las distancias de cualquier punto de la elipse a los focos es constante y ésta es igual a dos veces el semieje mayor:
  

• Semieje menor: longitud del segmento OJ o OL (b). Ambos semiejes son los dos ejes de simetría de la elipse. Se cumple que:
  
  Como vemos en el dibujo, esta relación cumple el teorema de Pitágoras.
• Radios vectores: los radios vectores de cualquier punto de la elipse (P=(x,y)) son los dos segmentos que lo unen con los dos focos. PF₁ y PF₂ (en el dibujo, d₁ y d₂).
• Vértices: son los puntos resultantes de la intersección de la elipse con la recta que pasa por los focos, F₁F₂, y su perpendicular que pasa por el centro. Es decir, son los puntos I, J, K y L

Ecuación de una elipse

ANUNCIOS

Los puntos pertenecientes a la elipse (x,y) son los puntos del plano que cumplen que la suma de su distancia a los dos focos es constante. La ecuación de la elipse es la siguiente:

En el caso de que la elipse esté centrada (el centro es el punto (0,0)), la ecuación es: