Parábola

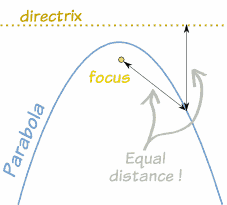
Una parábola es una curva en la que los puntos están a la misma distancia de: 

• Un punto fijo (El foco).
• Una linea fija (La directriz)

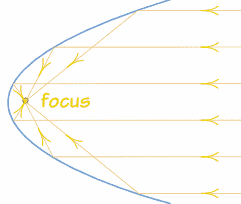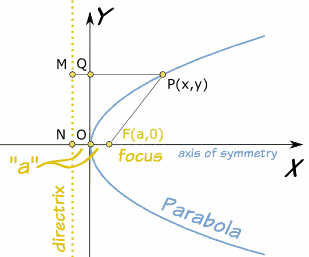
Y la parábola tiene la siguiente propiedad sorprendente: Reflector: Un rayo paralelo al eje de simetría se refleja en la superficie directamente hacia el foco. Así las parábolas se pueden usar para: antenas (antena parabólica), radares, concentrar los rayos solares para calentar un punto, los espejos dentro de focos y linternas Sus respectivas ecuaciones: Si pones la parábola en sus cordenada cartesianas (gráfico x-y) con: el vértice en el origen "O" y el eje de simetría en el eje x, entonces la curva queda definida por la ecuación: y2 = 4ax Las ecuaciones de las parábolas en las distintas orientaciones son: 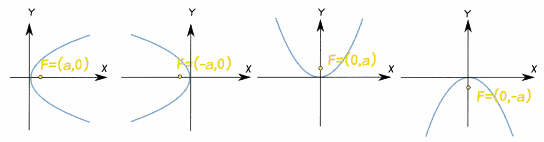y2 = 4ax y2 = -4ax x2 = 4ay x2 = -4ay